My friend Justin Simpson reached out to me asking if I could help with a Magic related math question (or is it a math related Magic question?). He wanted to know what the optimal deck construction was for a deck with nothing but mountains and Lightning Bolts, but with 99 card decks and 40 life instead of 60 & 20, presumably for some EDH-related metrics.
My first thought was, well Frank Karsten already solved this problem here, so it should be easy to adapt the logic he used to see what the EDH equivalent results are.
While trying to figure this out and answer Justin's question, I realized two important things. The first was that Frank's original code was written in Java, which I don't really know anything about. That meant my first step was to adapt his logic to Python, my preferred language. The second was that this original experiment was run in 2013, so it was using the Paris mulligan (i.e. not even the Vancouver mulligan with the free scry). Surely the London mulligan makes a difference, right?
Well, it definitely does in that the logic for the simulator is not nearly as straightforward. Frank's original Paris mulligan code used this policy:
If it is a hand with 7, 6 or 5 cards and it contains exactly 1, 2, or 3 mountains, keep. Otherwise, mulligan.
If it is a hand with 4 cards, keep.
That policy is pretty simple to implement, code-wise. If you had to make it Vancouver instead of Paris, you'd have to write another piece of code that looked at the top card of your deck after you kept, and decided whether to put it on the bottom or not. That would make it a bit more cumbersome, but still straightforward in the end - I'd probably use a policy that looked something like, if I have 2 or more lands in hand, put a land on the bottom and keep a bolt on top, and if I only have 1 land put a bolt on the bottom and keep a land on top.
What about London though? You get a fresh 7 card hand every time you mulligan, and after you keep you have to decide which cards to put on the bottom (although technically I think the rule plays out such that you put cards on the bottom before you announce keep or mulligan, which is a really clunky - hopefully anyone that has any rules influence reads this, realizes that how the rule is worded isn't how it's played out in practice and suggests the appropriate change). That's harder to do, because for every possible 7 card hand, you have to decide what the best 6 (or fewer) cards in it are. Some hands it's more obvious, like if you mulligan once and draw 4 bolts 3 mountains, you'd keep and put a land on the bottom. What if you mulliganed to 5 and drew 5 bolts 2 mountains though? Are you better off with 3 bolts and 2 lands, or 4 bolts and 1 land? If you mulliganed to 1 card, are you better off keeping a land, or a bolt?
I don't know how to answer all of those questions, and my next step in updating the logic was to implement a London mulligan policy. I took a stab at it myself by making an 8x7 grid of all possible starting hands and deciding what I would do with each of them, but I found that to be unsatisfying. Then I realized, I could just simulate absolutely everything. Thus was the first of my simulations.
gameplay logic
The actual gameplay logic is really easy. I borrowed Frank's logic and rewrote it from Java to Python. The algorithm looks something like this:
While the opponent's life is greater than zero:
-Add 1 to the turn counter
-If it's turn 1:
--If you have one or more lands in hand, add one to play and subtract one from your hand.
--If you have one or more bolts in your hand, subtract one from your hand and subtract 3 life from opponent's life total.
-If it's after turn 1:
--Draw a card and increase your hand count accordingly (+1 for lands or bolts).
--If you have one or more lands in hand, add one to play and subtract one from your hand.
--If you have more bolts than lands in play, subtract bolts from your hand equal to lands in play, and subtract 3 times that number from opponent's life total.
--Otherwise, subtract all bolts from your hand and subtract 3 times that number from opponent's life total.
Repeat this as many times as you want and after each time, record key stats such as turn counter, and number of mulligans.
the simulation
I simulated this 100,000 times, for each possible opening hand (there are 36 total - every mix of lands and bolts for each hand size from 0 to 7), and again for each plausible deck construction (I went as high as 52 bolts / 8 mountains and as low as 36 bolts / 24 mountains).
Here are the results, sorted by average kill turn, for Frank's original optimal deck of 44 bolts 16 mountains (which had an average kill turn of 4.91):
(Ignore the rightmost two columns - they're faulty. They represent the average kill turn of all hands and all 5+ card hands, but not all of these hands are equally likely. I was trying to come up with some measure of which deck performed best overall.)
You can see that for 44/16, the best four opening hands you can get, in order, are 5 bolts 2 mountains, then 4/3, then 4/2 (!!!), then 6/1. Going further down, you can see that a 5 card hand of 4 bolts 1 mountain is slightly faster than a 7 card hand of 3 bolts 4 mountains.
Compare these results to 42 bolts and 18 mountains:
42/18 is the most number of bolts you can have in your deck and have the 3 best 7 card hands be definitively better than every possible 6 card hand. Right away, we've learned something about the London mulligan before we're even done running simulations:
The specific construction of your deck has a meaningful impact on the mulligan policy you should implement.
Even though both decks have the same exact strategy and gameplay logic, adding two more lands to your deck means that you should have some serious considerations for how you plan to mulligan.
This result was super interesting to me, but it still didn't actually help me come up with the perfect mulligan policy - if I'm goldfishing 44/16 and staring at a 7 card hand of 6 bolts 1 mountain and I KNOW that 4/2 is faster, should I mulligan and try to look for it? This exact question was the inspiration for the poll I ran on Twitter:
You are goldfishing a deck with 44 Lightning Bolts and 16 Mountains. A supercomputer has informed you that a 6 card starting hand of 4 bolts, 2 mountains kills faster on average than the 7 card opener you’re looking at, 6 bolts 1 mountain.
— Alex Majlaton (@AlexMajlaton) October 14, 2020
London mulligan.
What do you do?
I ran this poll knowing what the "correct" answer was. I found that answer by designing the best mulligan policy I could think of, being informed by the above results.
an updated London mulligan policy
My logic looked something like this:
If you haven't mulliganed and you have 4 or 5 bolts, keep. Otherwise, mulligan.
If you've mulliganed once and have 4, 5, or 6 bolts, keep and start with 4/2 if you can, otherwise 5/1.
If you've mulliganed twice and have 3-6 bolts, keep and start with 4/1 if you can, otherwise 3/2.
If you've mulliganed 3 times, keep and start with 3/1 if you can, otherwise as many bolts as you have (which may be 4 bolts).
On top of that, I added a tracking mechanism for 4 card hands that I thought were "bad" (i.e. not 3/1) - I'd maybe prefer to mulligan these even further, but I didn't want to keep digging deeper into a mulligan policy where I thought the cases weren't very likely. If they came up more frequently than I'd like, then I'd rethink the policy, but I was satisfied by seeing how often each deck actually ended up starting with a "bad" 4 card hand (or even a 4 card hand at all).
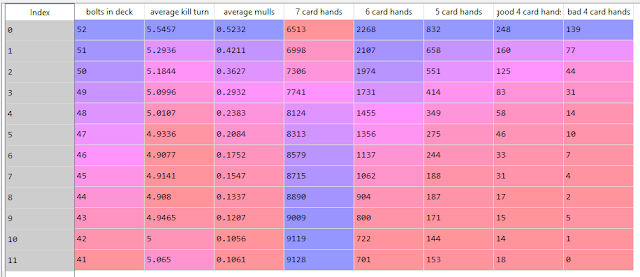
Note that the above policy is deciding to throw a 6/1 opener away in favor of looking for 4/2. I simulated 10,000 hands with this policy for each deck. Here are the results of that policy:
This table has a lot of interesting things going on:
-First, we can see that the original optimal Frank configuration of 44/16 is just about the same speed as it was before (just a hair faster even - 4.9059 vs. 4.910, basically identical if you round up).
-Next, we can see that it isn't even the fastest configuration using this policy - 47/13, 46/14, and 45/15 are all faster, with 45/15 being the fastest.
-We can see that average kill turn is parabolic and has a minimum at 45/15, but average mulls is strictly decreasing and 7 card hands is strictly increasing. 6 card hands, however, is not - its maximum is at 51/9.
I think this demonstrates that this blanket policy is not necessarily optimal for every configuration listed here - I'd be willing to bet there are some adjustments, possibly at the 6- and 5- card level, that would improve the performance of some of the higher density bolt decks at the expense of the lower density ones, or vice versa.
Now let's see what happens if you take the same exact mulligan policy, but instead of taking a mulligan with 6/1, you keep it instead:
Lots more interesting info here too:
-The original Frank 44/16 configuration is on top again, and is the fastest deck we've seen so far - 0.07 turns faster than its Paris mulligan counterpart.
-Decks with 15 or more lands all got a bump in speed, while decks with 14 or less took a performance hit. This confirms my suspicion above, that neither policy is strictly better than the other for every configuration.
-The number of 4 card hands is cut pretty much in half for every configuration. In other words, by removing one 7 card hand from your keep range, you nearly double the likelihood that you'll have to mulligan to 4.
Just for fun, let's see what happens if we add 3 bolts 4 mountains to our 7 card keep range:
-The decks mostly got slower. 51/9 got faster.
-46/14 is now pretty much tied with 44/16 for speed.
-Some decks have mulls to 4 cut roughly in half again, while others see no real change in mulls to 4.
Looking at all 3 tables side by side demonstrates that it's definitely possible to be too loose with keeping hands, as well as mulliganing too aggressively. I'd be willing to believe the policy I have is not optimal even for the fastest configuration so far (44/16, keep 4-5-6 bolts on 7) - there may be some tweaks at 5 cards and below that increase the speed even further.
the poll results
The poll I ran on Twitter only had ~100 responses, and of those, only ~75% had the guts to answer one way or the other. Still, the results from those responses were around 2 to 1 in favor of mulliganing 6/1 in favor of looking for 4/2. It's possible that I led people into the "wrong" answer with the way my poll was worded, but the poll results led me to another conclusion:
We probably don't understand how to use the London mulligan optimally yet.
The London mulligan rule is still very new - it's a bit over a year old, and maybe the last six months or so don't count because live tournaments haven't really been a thing (combined with dreadful Standard formats that have resulted in many bans). It's possible that we just aren't making optimal decisions with it yet.
These decisions go way beyond just opening up a hand and deciding whether it's playable or not. When you draw a starting hand of 6 bolts and 1 mountain, your thought process ought to be a bit deeper than "this is a 1 lander, if I miss land drops I'm screwed and I'm gonna lose, mulligan" or "if I topdeck a land I'll be in great shape, keep!" Ideally you've thought ahead of time about what you're going to do with hands like these while you were building and tweaking your deck.
Another important thing to keep in mind is that mulligans tend to lead to more mulligans. If I had to guess, I'd say that one of the reasons that keeping 6/1 is better than looking for 4/2 even though we know 4/2 is faster is that 4/2 is not so much faster that it overcomes all the times where you mulligan 6/1 and don't find it - you get another 6/1, or a hand with 3 or fewer bolts and the better move is to mulligan again.
This reminds me of a previous blog post I made about Affinity, and deciding beforehand that I would mulligan more aggressively into hands that start with 2 mana. I got a much better performance out of Affinity for that tournament with that mindset, so it's an easy sell for me that the last few steps of building or tweaking any constructed deck ought to be considering what your mulligan policy should be in general, and seeing if that policy necessitates any extra tweaks. That tournament with Affinity was the last time I really thought about mulligans as I was building my deck and it was before London, so the calculus is probably meaningfully different now.
There's some brute force math that can be done here with the hypergeometric distribution to determine how frequently each hand shows up, but I'll leave that to anyone that's really curious. I couldn't think of a good way to gauge the value of 6/1 relative to the average 6 card hand.
Allen Wu suggested the idea of a reinforcement learning engine, to try and make the computer figure out the optimal mulligan policy for any given deck construction. I think this would be an absolute blast to build, but it's a bit outside my skill set for right now - I'd have to learn how to teach an agent to mulligan and put cards on the bottom, and then come up with some scoring mechanism to make sure it understands that it's trying to optimize for speed.
If it were built though, it would probably be versatile enough to incorporate all of Frank's original gameplay logic for more sophisticated aggro decks - the ones with 1 drops, 2 drops, and so on. It would be interesting to see a deep learning engine attack those strategies.
Sticking to the existing program, some other questions that would be interesting to answer would be what kind of gains you could get from tightening the mulligan policy at the 4-card level and below. I'd also be curious about what the various performances are under the Vancouver mulligan. My guess would that be London is the best overall mulligan system for pulling the best performance out of the bolt deck, but I'd be curious to see how much of an improvement over Vancouver it offers, if any.
In case you're curious about Justin's original EDH-flavored question, using the best London policy that I found above, the optimal 99 card configuration for a 40 life game is 85 bolts and 14 mountains, which has an average kill turn of 12.5031.
My source code is here.
Shout outs go to Frank Karsten for laying all the groundwork for this analysis, and to Justin Simpson for being the inspiration for it.




My sense for the question opened at the end of the first 'future research ideas' is that it should just be the greater of 6/1's modeled turn and the weighted average modeled turns of all the 6 card hands. What might be wrong with that approach?
ReplyDelete